534 字
3 分钟
青岛市2022编程市赛 T3结论与简易证明
首先,结论与证明来自http://oeis.org/A005732/a005732.pdf,这里给出简单翻译和加工
结论
给出结论,在一个圆上取 个点相连,构成的三角形个数为
证明
如何证明呢,我们不妨从圆上n个点中的任意个可以构成几个三角形来入手,我们先看7个点的图,来观察一下! 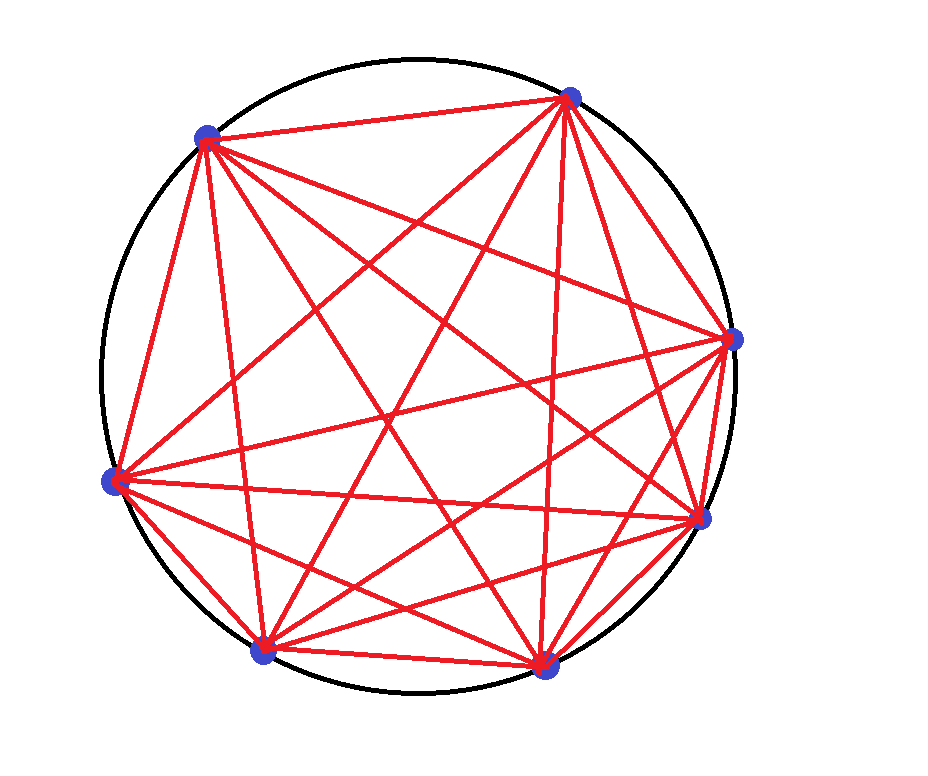
如果你有十足的耐心的话,你可以数出来,这是 个三角形
但是,我们要求出一个通项公式,我们可以发现,每一个三角形都是由多个或 个圆上的点组成的,让我们通过这个分类讨论
推柿子
首先tips:认识到圆“上”的概念:就是在圆的边上
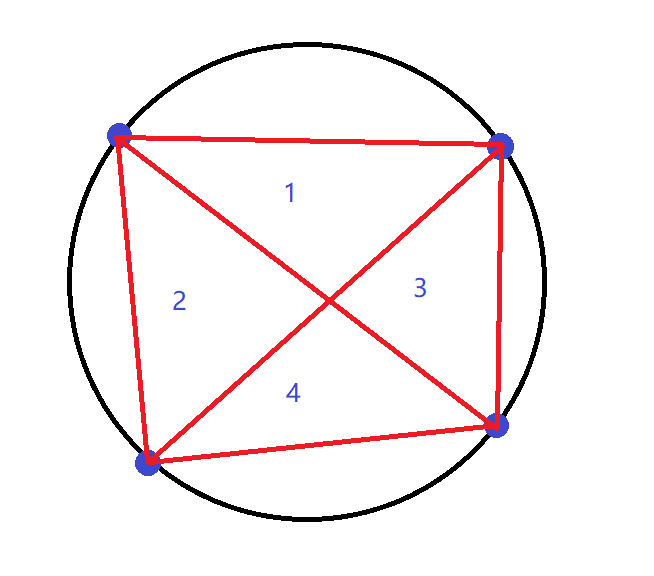
- 由圆上 个点构成的三角形有 个。证明:圆上每三个点可以构成一个三角形,反之亦然.(这个不用画图了吧qwq)
- 只由圆上 个点 和另外 个点 构成的三角形个数有 个。证明:对于圆上的每 个点,可以构成 个”有 个点在圆上” 的三角形
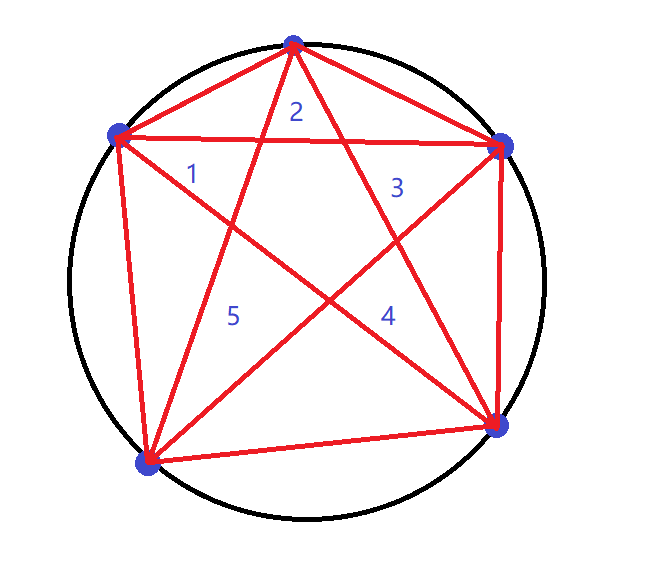
- 只由圆上 个点 和另外 个点 构成的三角形个数有 个。证明:对于圆上的每 点,可以构成 个”有 个点在圆上” 的三角形
- 只由圆上 个点 和另外 个点 构成的三角形个数有 个。证明:对于圆上的每 点,可以构成 个”有 个点在圆上” 的三角形
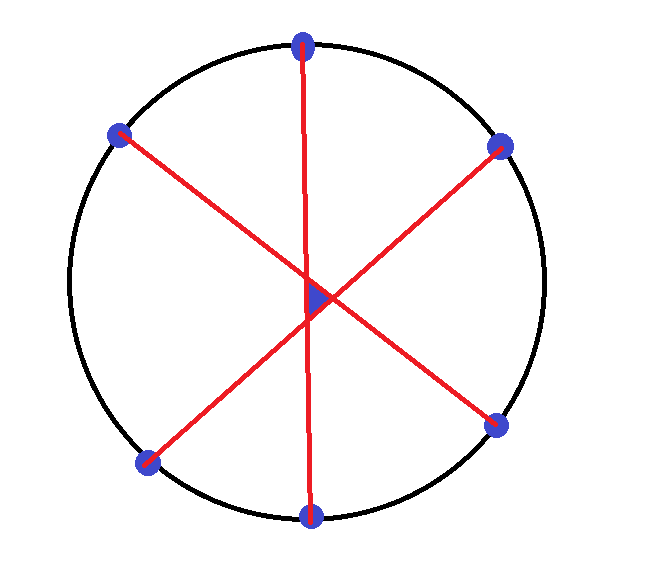 (当然,这个图里还有别点之间的的连线,只不过我懒得画了emmmm)
(当然,这个图里还有别点之间的的连线,只不过我懒得画了emmmm)
整理柿子
最后,就是整理这个式子了(挺复杂的qwq)(参考this)
青岛市2022编程市赛 T3结论与简易证明
https://blog.histcat.top/posts/counterattack/ 